Computer Vision Project 5

Author: Minshen Zhang, Student Email: 3036648523@qq.com

Part 1: Fit a Neural Field to a 2D Image

[Implement: Network]

In this section, I implemented a pytorch nn.Module class described in the following graph:

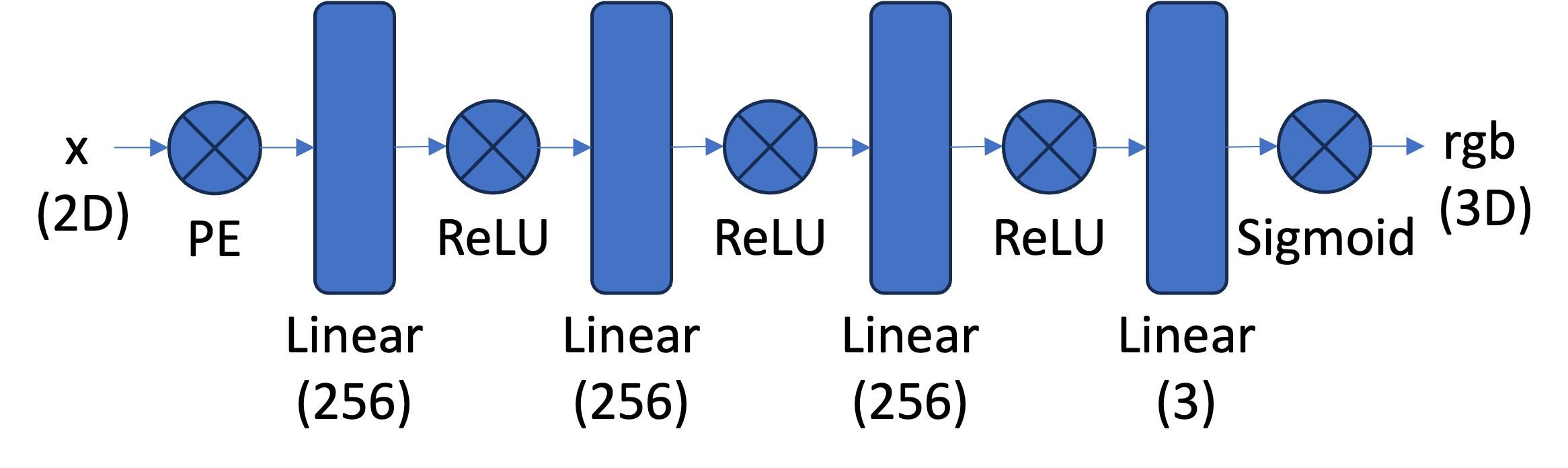
Positional Encoding

The following code is how I implement the Positional Encoding by numpy to speed up (initially I implemented the positional encoding by for-loop, and it’s very slow…)

class PosEncoding(nn.Module):
    def __init__(self, L):
        super(PosEncoding, self).__init__()
        self.L = L
        self.d_model = 4 * L + 2
        
    def forward(self, x):
        batch_size = x.shape[0]
        result = torch.zeros(batch_size, self.d_model, device=device)
        result[:, 0] = x[:, 0]
        result[:, 1] = x[:, 1]
        positions = torch.arange(0, self.L, device=device).unsqueeze(0).expand(batch_size, -1).float()
        result[:, 2:2*self.L + 2:2] = torch.sin(2 ** positions * np.pi * x[:, 0].unsqueeze(1))
        result[:, 3:2*self.L + 3:2] = torch.cos(2 ** positions * np.pi * x[:, 0].unsqueeze(1))
        result[:, 2*self.L+2:4*self.L + 2:2] = torch.sin(2 ** positions * np.pi * x[:, 1].unsqueeze(1))
        result[:, 2*self.L+3:4*self.L + 3:2] = torch.cos(2 ** positions * np.pi * x[:, 1].unsqueeze(1))
        return torch.tensor(result, dtype=torch.float32).to(device)

Nerf2D network

class Nerf2D(nn.Module):
    def __init__(self):
        super(Nerf2D, self).__init__()
        L = 10
        d_model = 4 * L + 2
        self.positional_encoding = PosEncoding(L)
        self.nerf = nn.Sequential(
            nn.Linear(d_model, 256),
            nn.ReLU(),
            nn.Linear(256, 256),
            nn.ReLU(),
            nn.Linear(256, 256),
            nn.ReLU(),
            nn.Linear(256, 3),
            nn.Sigmoid()
        )  # from (batch_size, d_model) to (batch_size, 3)

    def forward(self, x):
        """
        :param x: it should be a tensor with shape (batch_size, 2(input_dim)))
        :return: 
        """
        x = self.positional_encoding(x)
        x = self.nerf(x)
        return x

[Implement: Dataloader]

The following code implements a pytorch dataset, and each time we fetch a data, it will randomly select 1/3 points from the original image, with corresponding RGB value:

class NerfDataset(Dataset):
    def __init__(self, image_path):
        super(NerfDataset, self).__init__()
        self.image = np.array(Image.open(image_path).convert("RGB"))
        self.width = self.image.shape[1]
        self.height = self.image.shape[0]
        
    def __len__(self):
        return 10
    
    def __getitem__(self, index, batch_size=200000):
        # randomly choose a point within the image
        x = np.random.randint(0, self.width, size=(batch_size, 1))
        y = np.random.randint(0, self.height, size=(batch_size, 1))
        points = np.concatenate([x, y], axis=1)
        rgb_values = np.array([self.image[point[1], point[0]] for point in points])
        # to float32
        points = points.astype(np.float32)
        rgb_values = rgb_values.astype(np.float32)
        # normalize
        points[:, 0] = points[:, 0] / self.width
        points[:, 1] = points[:, 1] / self.height
        rgb_values = rgb_values / 255
        return torch.tensor(points), torch.tensor(rgb_values)

# ...

dataloader = DataLoader(dataset, batch_size=1000, shuffle=True)

[Implement: Loss Function, Optimizer, and Metric]

The following code defines the Loss Function, Optimizer, and model.

loss_function = MSELoss()
model = Nerf2D().to(device)
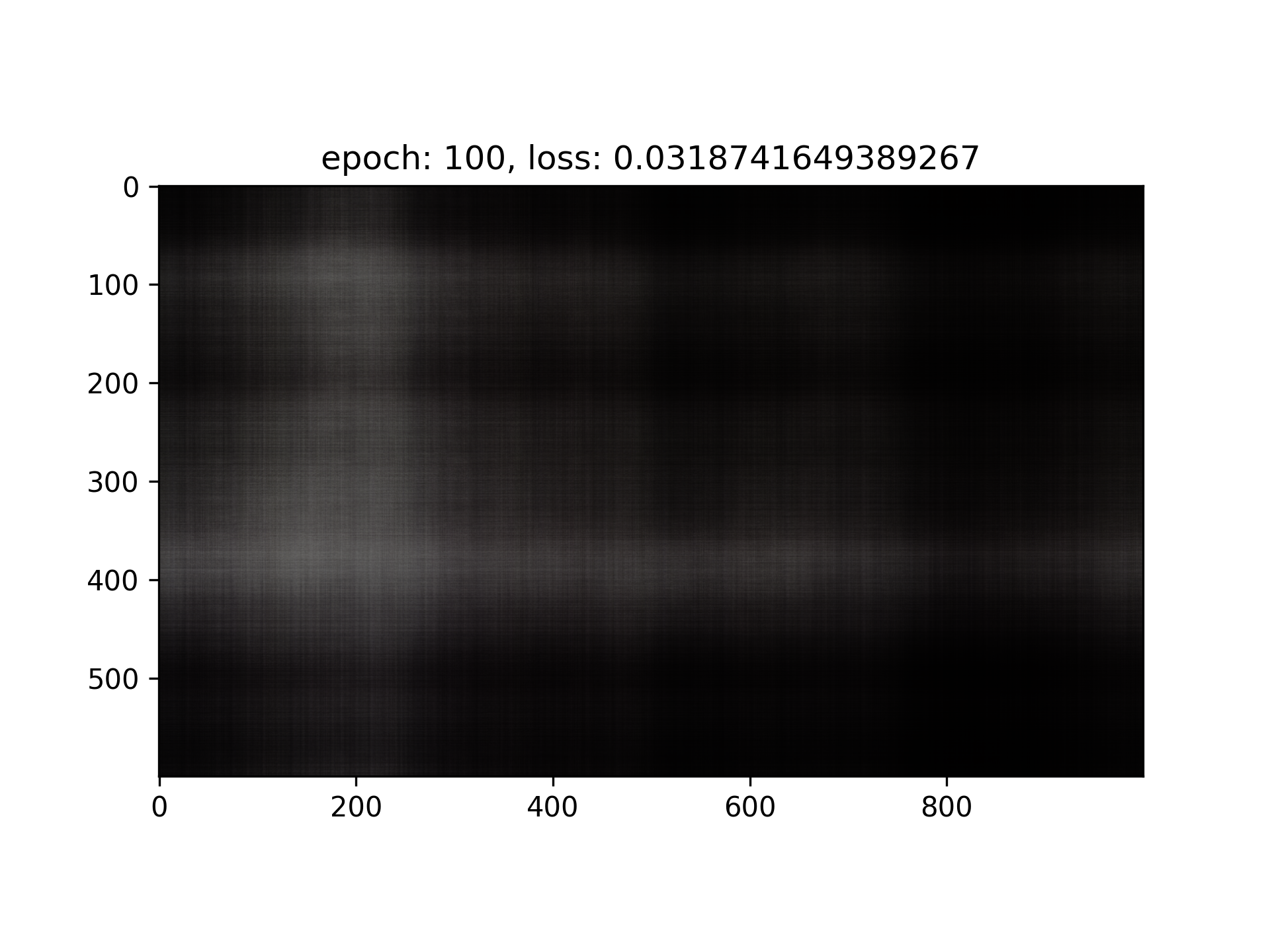
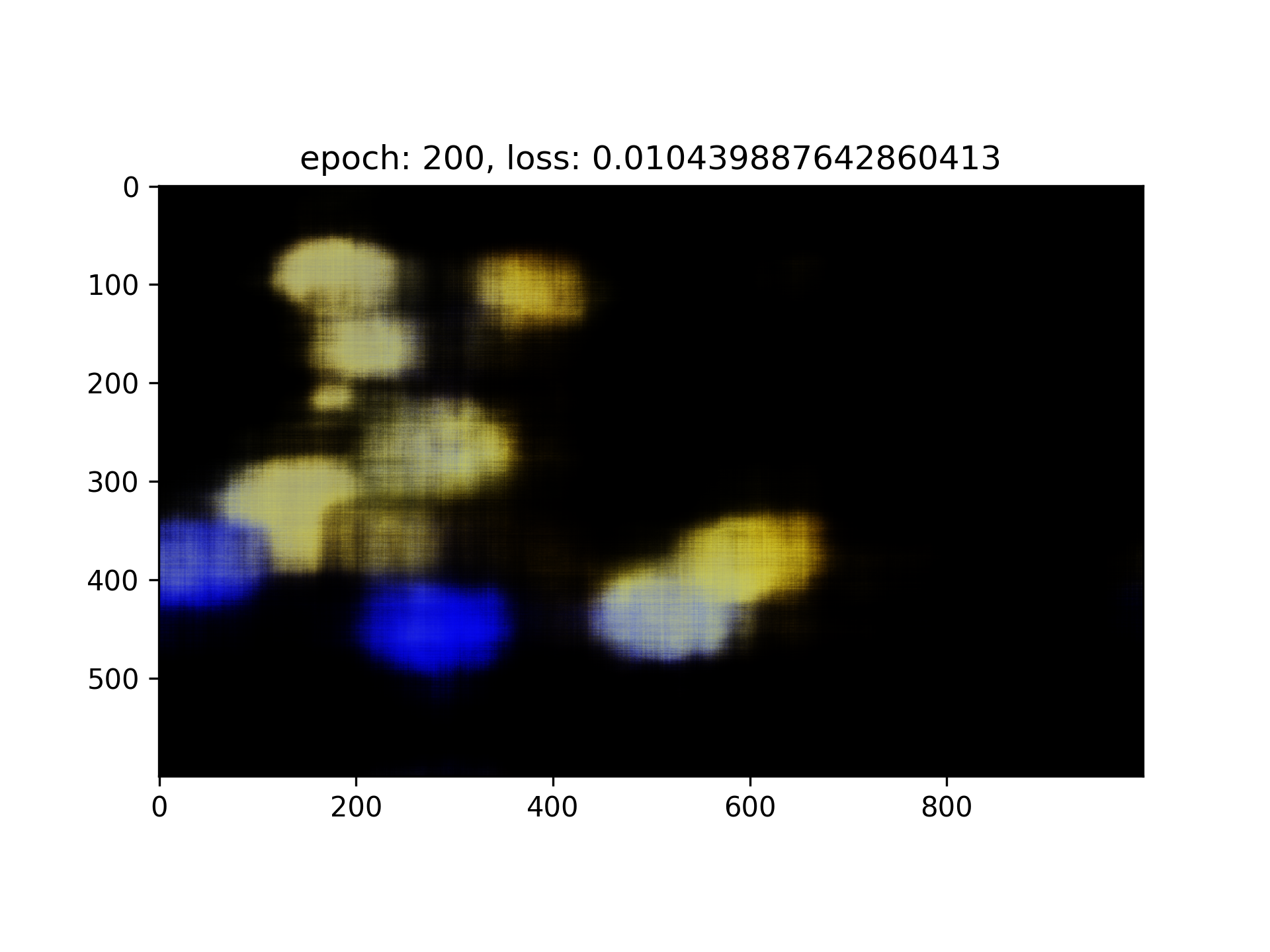
optimizer = Adam(model.parameters(), lr=1e-2)

Training Result(lr=1e-2, L=10, layers = 4(default))

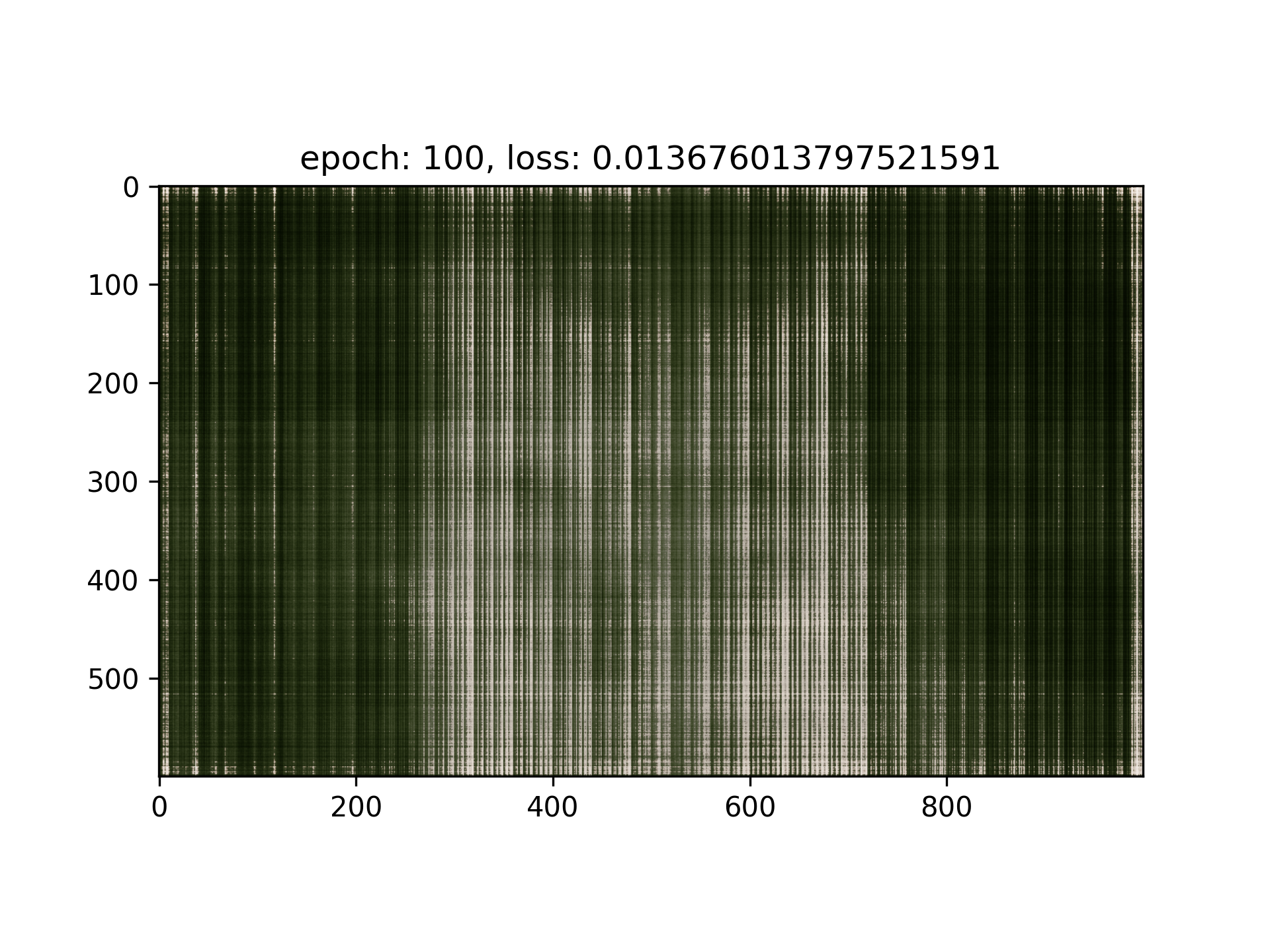
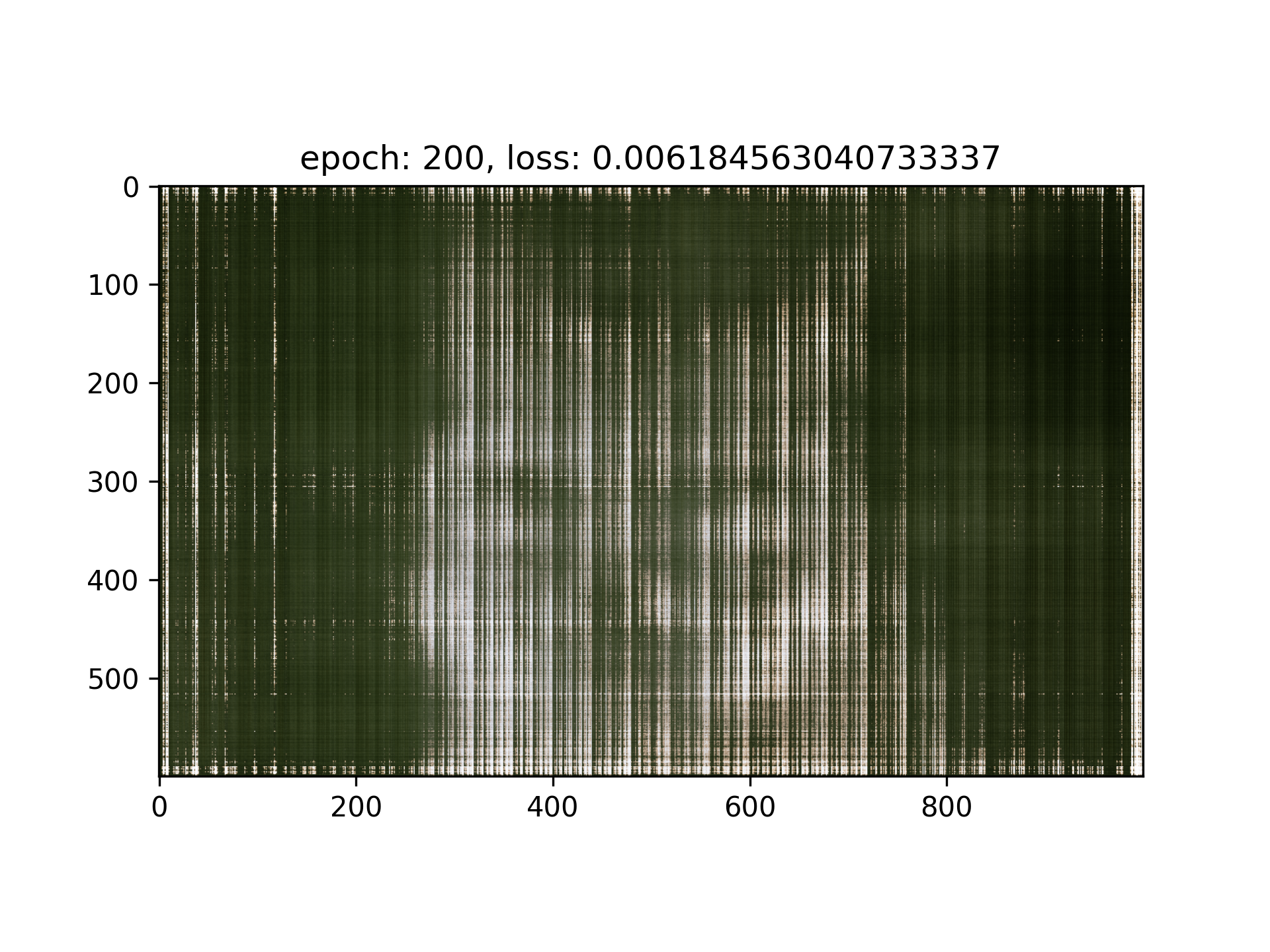
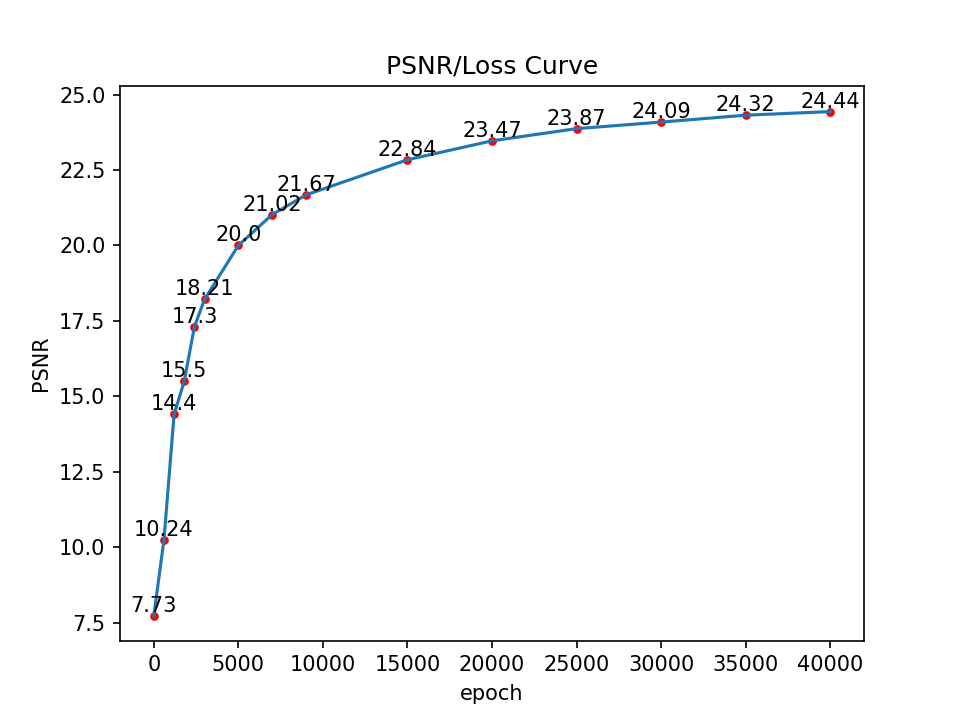
Metrics

Iteration = 1000, MSE Loss = 0.8643298, PSNR = 0.6332051331896413

Iteration = 3000, MSE Loss = 0.058173921, PSNR = 12.352716631867715

Iteration = 5000, MSE Loss = 0.0054667368, PSNR = 22.62271835027278

Curve

[Implement: Hyperparameter Tuning]

Tuning Learning rate

I tried to tune the learning rate to 1e-3, and it seems like there’s no major difference.

I think the reason is that Adam Optimizer will automatically handle the best learning rate for every parameters, so that the initial learning rate doesn’t matter too much.

Tuning Positional Encoding L & Number of layers

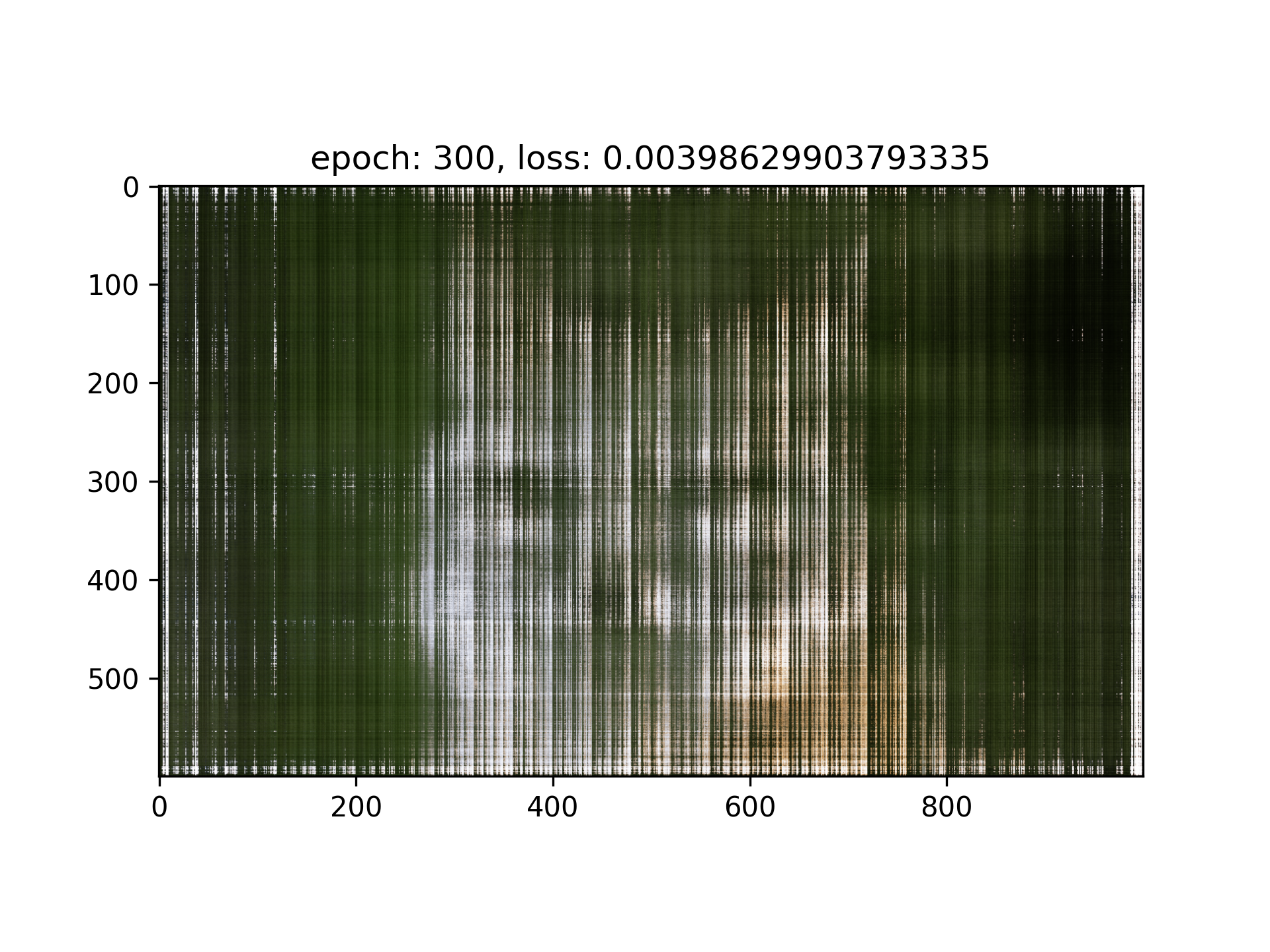
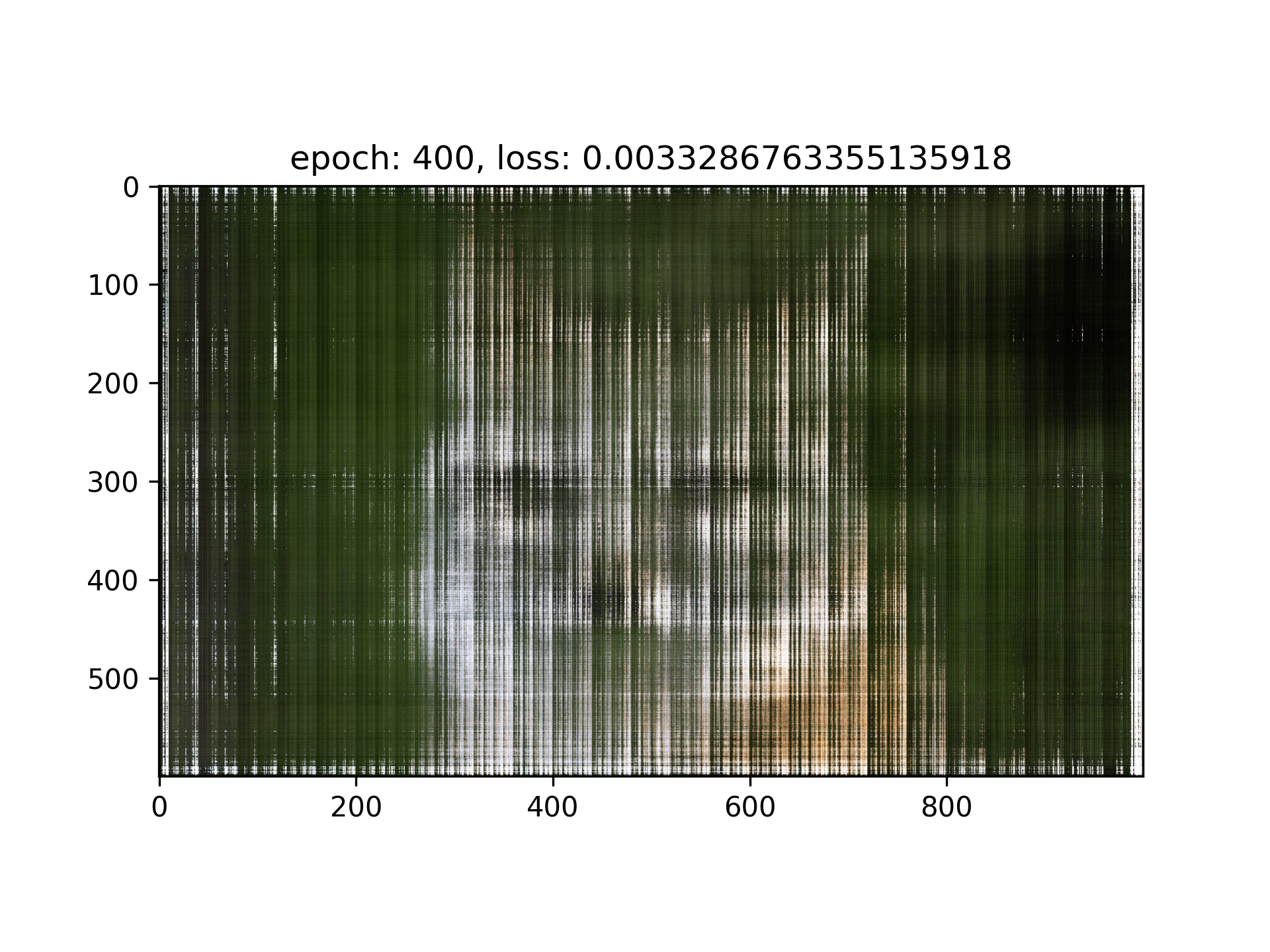
I observed that in my result of Iteration = 5000, the loss seems stuck in the order of magnitude of 1e-3, I think it’s majorly because of the positional encoding doesn’t have high enough frequency, and the network is not deep enough the handle the entire image, therefore I tried with this setting: (lr=1e-3, L=20, layers = 7)

💡

To be mentioned, the number of iteration = 10 * epoch.

Uh...Seems like it’s worse, maybe we should still use the original hyperparameters : (

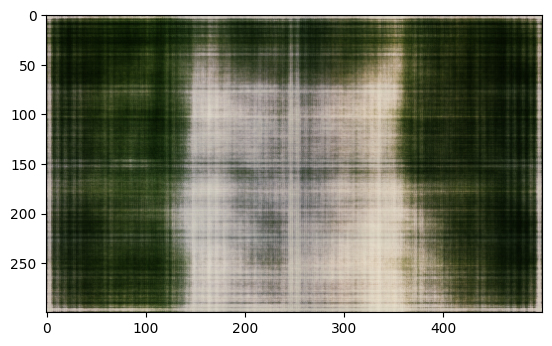
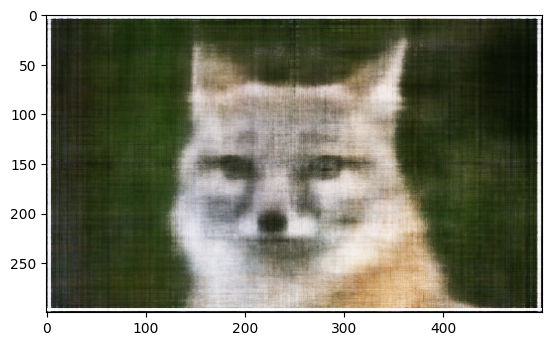
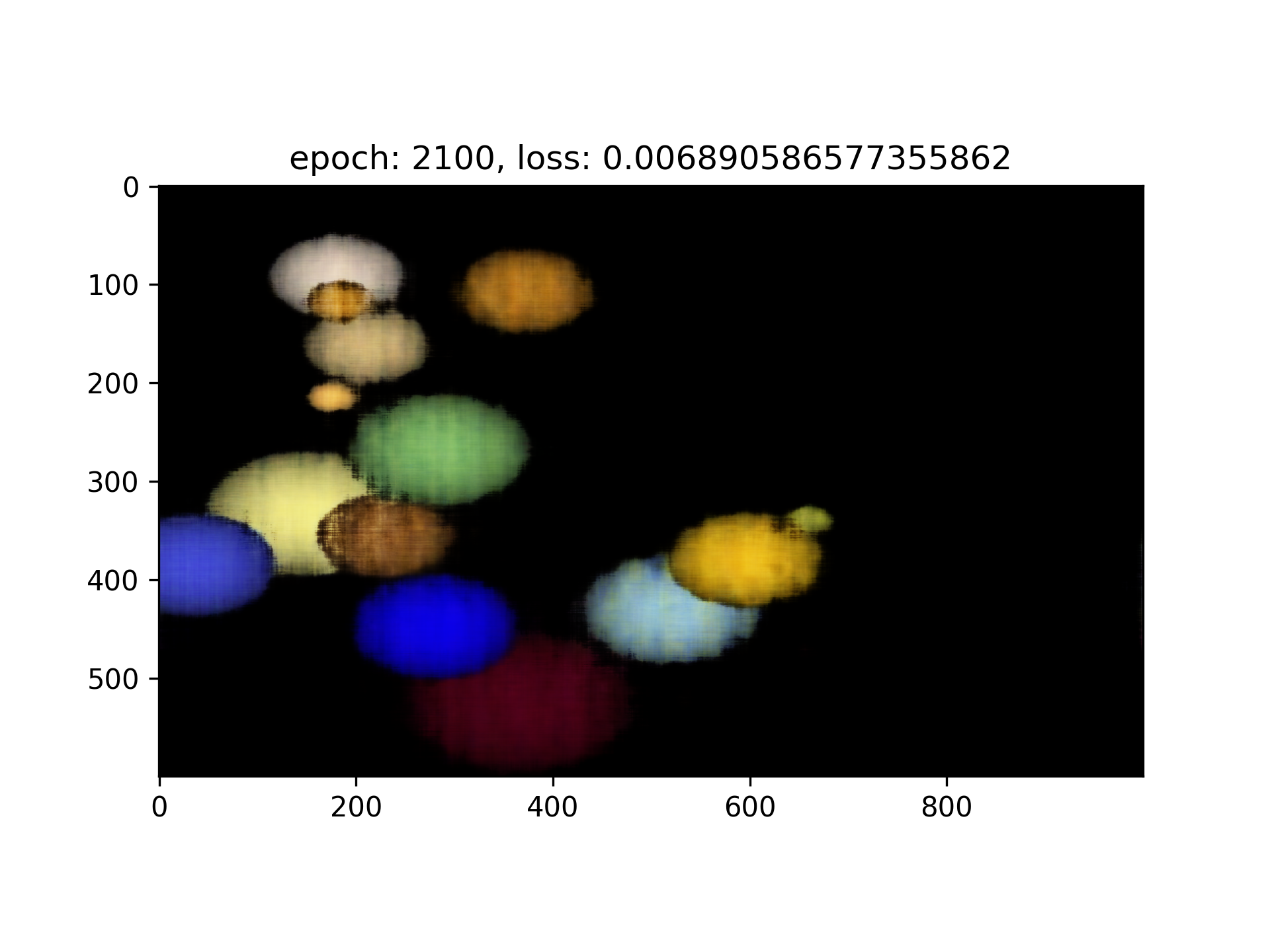
Training on my own image

Ground Truth

Result

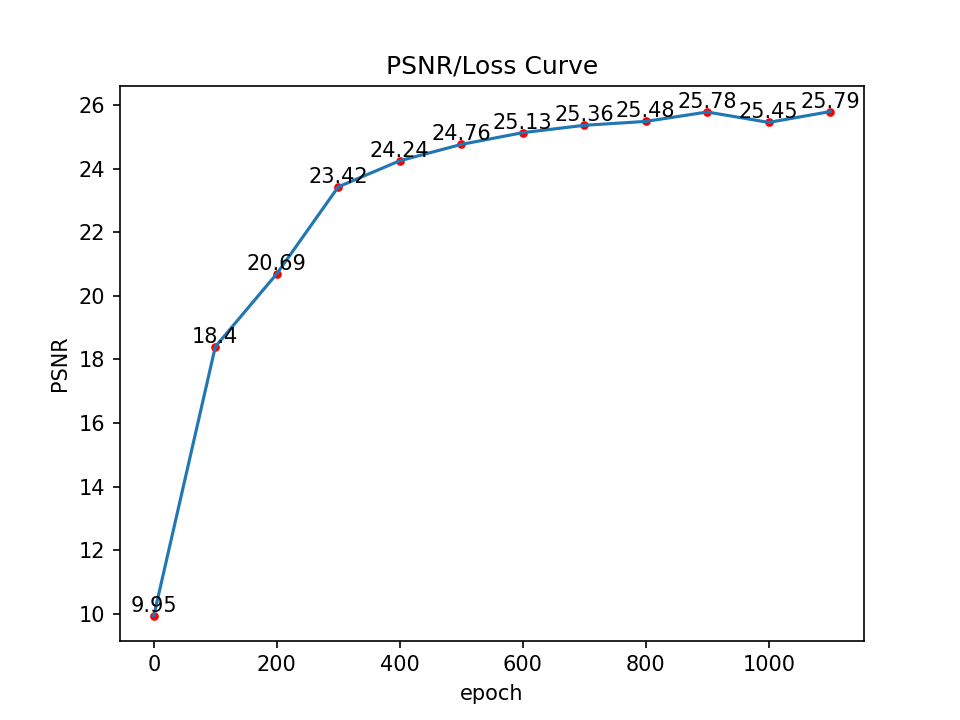
PSNR Curve

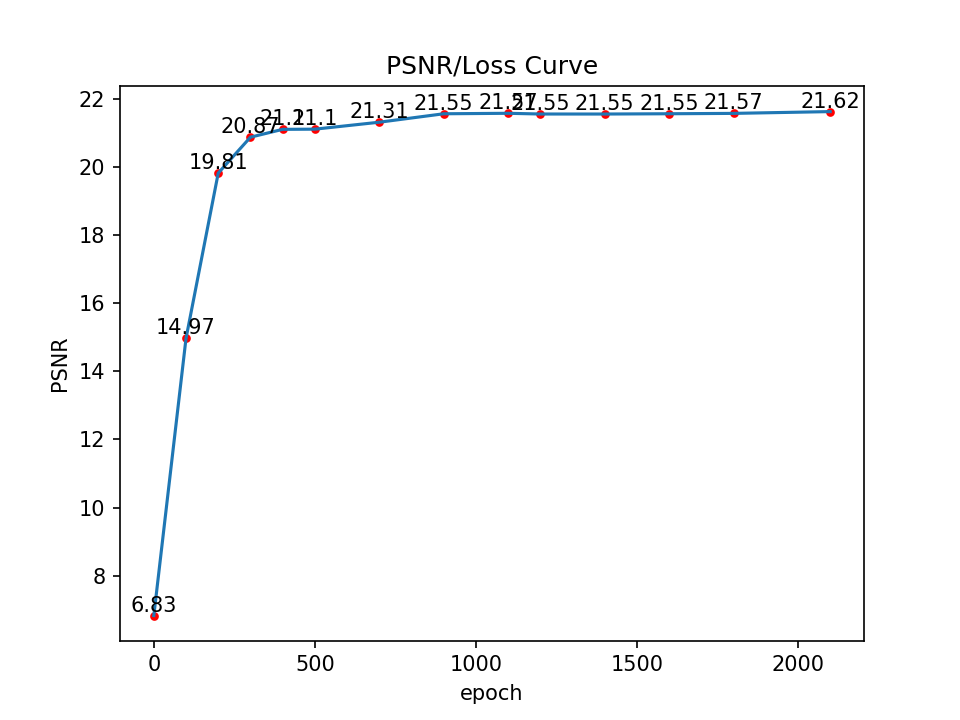
Part 2: Fit a Neural Radiance Field from Multi-view Images

Part 2.1: Create Rays from Cameras

Function: `transform(c2w, x_c)`

def transform(c2w, x_c):
    """
    Transform a point from camera coordinate system to world coordinate system.
    Args:
        c2w: Camera-to-world transformation matrix. Shape: [batch_size, 4, 4]
        x_c: Point in camera coordinate system. Shape: [batch_size, 3]
    Returns:
        x_w: Point in world coordinate system. Shape: [batch_size, 3]
    """
    ones = torch.ones((x_c.shape[0], 1)).to(device)
    x_c_homogeneous = torch.cat((x_c, ones), dim=1)
    x_w_homogeneous = torch.matmul(c2w, x_c_homogeneous[:, :, None])
    x_w = x_w_homogeneous[:, :3, 0] / x_w_homogeneous[:, 3, 0][:, None]
    
    return x_w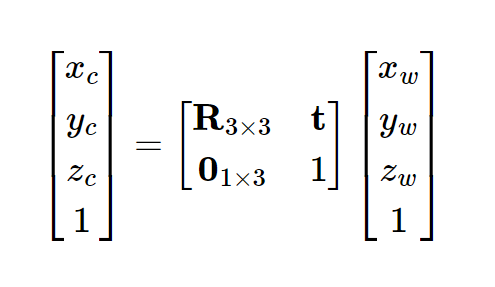

💡

Apply the test of assert x == transform(c2w.inv(), transform(c2w, x)) indicates that this function is well-implemented!

Function: `pixel_to_camera(K, uv, s)`

def pixel_to_camera(K, uv, s):
    """
    Transform a pixel coordinate to camera coordinate system.

    Args:
        K: Camera intrinsic matrix. Shape: [3, 3]
        uv: Pixel coordinate. Shape: [batch_size, num_pixels, 2]
        s: Depth. Shape: [batch_size, num_pixels]

    Returns:
        x_c: Point in camera coordinate system. Shape: [batch_size, num_pixels, 3]
    """
    batch_size, num_pixels, _ = uv.shape
    uv_homogeneous = torch.cat((uv, torch.ones(batch_size, num_pixels, 1).to(device)), dim=-1)
    K_inv = torch.inverse(K)
    
    x_c_homogeneous = torch.einsum('ij,bkj->bki', K_inv, uv_homogeneous)
    x_c = x_c_homogeneous * s.unsqueeze(-1)
    
    return x_c

Here is an explanation of the pixel_to_camera function:

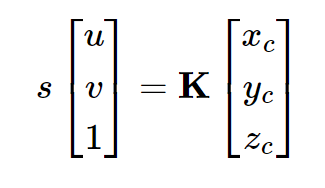
uv_homogeneous = torch.cat((uv, torch.ones(batch_size, num_pixels, 1).to(device)), dim=-1) - This creates a tensor uv_homogeneous by concatenating the uv tensor with a tensor of ones, resulting in a tensor with shape [batch_size, num_pixels, 3]. The added ones represent the homogeneous coordinate of the pixel coordinates.

x_c_homogeneous = torch.einsum('ij,bkj->bki', K_inv, uv_homogeneous) - This line performs matrix multiplication between the inverse intrinsic matrix K_inv and the uv_homogeneous tensor using the Einstein summation convention. It results in a tensor x_c_homogeneous with shape [batch_size, num_pixels, 3], representing the coordinates of the pixels in the camera coordinate system.

Function: `pixel_to_ray(K, c2w, uv)`

def pixel_to_ray(K, c2w, uv):
    """
    Transform a pixel coordinate to a ray in world coordinate system.
    Args:
        K: Camera intrinsic matrix. Shape: [3, 3]
        c2w: Camera-to-world transformation matrix. Shape: [batch_size, 4, 4]
        uv: Pixel coordinate. Shape: [batch_size, num_pixels, 2]
    Returns:
        ray_o: Ray origin(camera location) in world coordinate system. Shape: [batch_size, num_pixels, 3]
        ray_d: Ray direction in world coordinate system. Shape: [batch_size, num_pixels, 3]
    """
    batch_size, num_pixels, _ = uv.shape
    R_3x3 = c2w[:, :3, :3]
    t_3x1 = c2w[:, :3, 3]

    ray_o = t_3x1
    s = torch.ones(batch_size, num_pixels).to(device)
    x_c = pixel_to_camera(K, uv, s)

    ray_d = torch.einsum('bij,bkj->bki', R_3x3, x_c)
    ray_d = ray_d / torch.norm(ray_d, dim=-1, keepdim=True)
    ray_o = ray_o.reshape(batch_size, 3)
    ray_o = ray_o[:, None, :].expand(-1, num_pixels, -1)
    return ray_o, ray_d

The pixel_to_ray function is used to transform a pixel coordinate to a ray in the world coordinate system. It takes in the camera intrinsic matrix (K), camera-to-world transformation matrix (c2w), and pixel coordinate (uv) as inputs.

R_3x3 = c2w[:, :3, :3] - This line extracts the rotation components from the c2w matrix. It selects the first three rows and three columns of the matrix, resulting in a 3x3 rotation matrix R_3x3.

t_3x1 = c2w[:, :3, 3] - This line extracts the translation components from the c2w matrix. It selects the first three rows and the fourth column of the matrix, resulting in a 3x1 translation vector t_3x1.

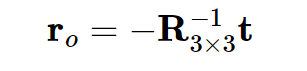
x_c = pixel_to_camera(K, uv, s) - This line calls the pixel_to_camera function to transform the pixel coordinates to camera coordinate system points (x_c).

ray_d = torch.einsum('bij,bkj->bki', R_3x3, x_c) - This line performs matrix multiplication between the rotation matrix R_3x3 and the camera coordinate system points x_c. It transforms the camera space points to world space rays.

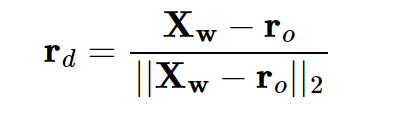
Part 2.2: Sampling

Function: `sample_rays(c2w, K, img, num_rays_per_image=10, hardcode_uv=None)`

def sample_rays(c2w, K, img, num_rays_per_image=10, hardcode_uv=None):
    """
    Sample rays from an image.

    Args:
        c2w: Camera-to-world transformation matrix. Shape: [batch_size, 4, 4]
        K: Camera intrinsic matrix. Shape: [3, 3]
        img: Input image. Shape: [batch_size, H, W, 3], the batch size will be M
        num_rays_per_image: Number of rays to sample from the image, this will equal to N // M
        hardcode_uv: if not None, we will use this uv to sample rays, shape: [batch_size, num_rays_per_image, 2]

    Returns:
        rays_o: Ray origin(camera location) in world coordinate system. Shape: [batch_size, num_rays_per_image, 3]
        rays_d: Ray direction in world coordinate system. Shape: [batch_size, num_rays_per_image, 3]
        rays_rgb: RGB values of the rays. Shape: [batch_size, num_rays_per_image, 3]
    """
    batch_size, H, W, _ = img.shape
    # print(f"sample_rays: batch_size={batch_size}, H={H}, W={W}")
    if hardcode_uv is None:
        uv = torch.rand(batch_size, num_rays_per_image, 2).to(device) * torch.tensor([W, H], dtype=torch.float32).to(device)
    else:
        uv = hardcode_uv
    rays_o, rays_d = pixel_to_ray(K, c2w, uv)

    rays_rgb = torch.stack([img[b, uv[b, :, 1].long(), uv[b, :, 0].long(), :] for b in range(batch_size)], dim=0)
    # rays_rgb = torch.stack([img[b, uv[b, :, 0].long(), uv[b, :, 1].long(), :] for b in range(batch_size)], dim=0)
    return rays_o, rays_d, rays_rgb

The sample_rays function is used to sample rays from an input image. It takes in the camera-to-world transformation matrix (c2w), camera intrinsic matrix (K), input image (img), and the number of rays to sample per image (num_rays_per_image) as inputs. Additionally, it has an optional argument hardcode_uv which is used for later rendering purposes.

if hardcode_uv is None: - This line checks if the hardcode_uv argument is None. If it is, the function proceeds to generate random pixel coordinates uv within the image bounds using torch.rand. Each coordinate is multiplied by the width and height of the image to ensure it falls within the valid range.

rays_o, rays_d = pixel_to_ray(K, c2w, uv) - This line calls the pixel_to_ray function to transform the pixel coordinates uv to rays in the world coordinate system. It calculates the ray origin rays_o (camera location) and ray direction rays_d based on the provided camera intrinsic matrix K and camera-to-world transformation matrix c2w.

rays_rgb = torch.stack([img[b, uv[b, :, 1].long(), uv[b, :, 0].long(), :] for b in range(batch_size)], dim=0) - This line retrieves the RGB values of the rays from the input image. It uses indexing to access the corresponding RGB values at the sampled pixel coordinates uv for each image in the batch. The RGB values are stacked together to form the rays_rgb tensor.

The sample_rays function returns the ray origin (rays_o), ray direction (rays_d), and RGB values (rays_rgb) of the sampled rays.

The hardcode_uv parameter allows for the option to provide specific pixel coordinates, which can be useful for rendering purposes later on.

Function: `sample_points_from_rays(rays_o, rays_d, near, far, num_samples_per_ray=64, train=True)`

def sample_points_from_rays(rays_o, rays_d, near, far, num_samples_per_ray=64, train=True):
    """
    Sample points from rays.

    Args:
        rays_o: Ray origin(camera location) in world coordinate system. Shape: [batch_size, num_rays_per_image, 3]
        rays_d: Ray direction in world coordinate system. Shape: [batch_size, num_rays_per_image, 3]
        near: Near plane. float
        far: Far plane. float
        num_samples_per_ray: Number of points to sample from each ray, this will equal to N // M

    Returns:
        points: Sampled points. Shape: [batch_size, num_rays_per_image, num_samples_per_ray, 3]
                if train is True, we will take random samples between near and far
                if train is False, we will take uniform samples between near and far
    """
    if train:
        z_vals = near + (far - near) * torch.rand(rays_o.shape[0], rays_o.shape[1], num_samples_per_ray).to(device)
    else:
        z_vals = torch.linspace(near, far, num_samples_per_ray).expand(rays_o.shape[0], rays_o.shape[1], num_samples_per_ray).to(device)

    points = rays_o.unsqueeze(2) + rays_d.unsqueeze(2) * z_vals.unsqueeze(-1)

    return points

The sample_points_from_rays function is used to sample points along the given rays in 3D space. It takes in the ray origin (rays_o), ray direction (rays_d), near plane (near), far plane (far), and the number of samples to take per ray (num_samples_per_ray) as inputs.

if train: - This line checks if the train flag is True. If it is, random samples are taken between the near and far planes using torch.rand and scaling the range with (far - near). The resulting z_vals tensor has a shape of [batch_size, num_rays_per_image, num_samples_per_ray].

If the train flag is False, uniform samples are taken between the near and far planes using torch.linspace. The resulting z_vals tensor has a shape of [batch_size, num_rays_per_image, num_samples_per_ray].

points = rays_o.unsqueeze(2) + rays_d.unsqueeze(2) * z_vals.unsqueeze(-1) - This line calculates the 3D points along each ray by adding the ray origin rays_o (broadcasted to have shape [batch_size, num_rays_per_image, num_samples_per_ray, 3]) with the element-wise product of the ray direction rays_d (broadcasted to have shape [batch_size, num_rays_per_image, num_samples_per_ray, 3]) and the z_vals tensor (broadcasted to have shape [batch_size, num_rays_per_image, num_samples_per_ray, 1]). The resulting points tensor has a shape of [batch_size, num_rays_per_image, num_samples_per_ray, 3] and contains the sampled 3D points.

The sample_points_from_rays function returns the sampled points along the rays in 3D space, represented by the points tensor.

Part 2.3: Putting the Dataloading All Together

# dataset = RaysData(images_train, K, c2ws_train)
class RaysData(torch.utils.data.Dataset):
    def __init__(self, images, K, c2ws):
        """
        Args:
            images: Input images. Shape: [M, H, W, 3]
            K: Camera intrinsic matrix. Shape: [3, 3]
            c2ws: Camera-to-world transformation matrix. Shape: [M, 4, 4]
        """
        self.images = images
        self.K = K
        self.c2ws = c2ws

    def __len__(self):
        return self.images.shape[0]

    def __getitem__(self, idx):
        img = self.images[idx]
        K = self.K
        c2w = self.c2ws[idx]
        rays_o, rays_d, rays_rgb = sample_rays(c2w, K, img, num_rays_per_image=1)
        return rays_o, rays_d, rays_rgb
    
    def sample_rays(self, max_idx, ray_per_image=64):
        # idx is from 0 to ray_num - 1, uniform step
        idx = torch.arange(max_idx)
        img = self.images[idx]
        K = self.K
        c2w = self.c2ws[idx]
        rays_o, rays_d, rays_rgb = sample_rays(c2w, K, img, num_rays_per_image=ray_per_image)
        return rays_o, rays_d, rays_rgb
    
    def sample_rays_random_batch(self, batch_size, ray_per_image=64):
        idx = torch.randint(0, self.images.shape[0], (batch_size,))
        img = self.images[idx]
        K = self.K
        c2w = self.c2ws[idx]
        # print(f"dataset: c2w.shape={c2w.shape}, img.shape={img.shape}")
        rays_o, rays_d, rays_rgb = sample_rays(c2w, K, img, num_rays_per_image=ray_per_image)
        return rays_o, rays_d, rays_rgb

    
    def sample_rays_idx(self, idx, ray_per_image=64):
        img = self.images[idx].reshape(1, *self.images[idx].shape)
        K = self.K
        c2w = self.c2ws[idx].reshape(1, *self.c2ws[idx].shape)
        rays_o, rays_d, rays_rgb = sample_rays(c2w, K, img, num_rays_per_image=ray_per_image)
        return rays_o, rays_d, rays_rgb
    
    def sample_rays_idx_hardcode_uv(self, idx, uv, ray_per_image=64):
        img = self.images[idx].reshape(1, *self.images[idx].shape)
        K = self.K
        c2w = self.c2ws[idx].reshape(1, *self.c2ws[idx].shape)
        rays_o, rays_d, rays_rgb = sample_rays(c2w, K, img, num_rays_per_image=ray_per_image, hardcode_uv=uv)
        return rays_o, rays_d, rays_rgb

The RaysData class is a simple dataset class used for handling input images, camera intrinsic matrices, and camera-to-world transformation matrices. It is designed to work in conjunction with the other functions in the code snippet.

Viser Output

💡

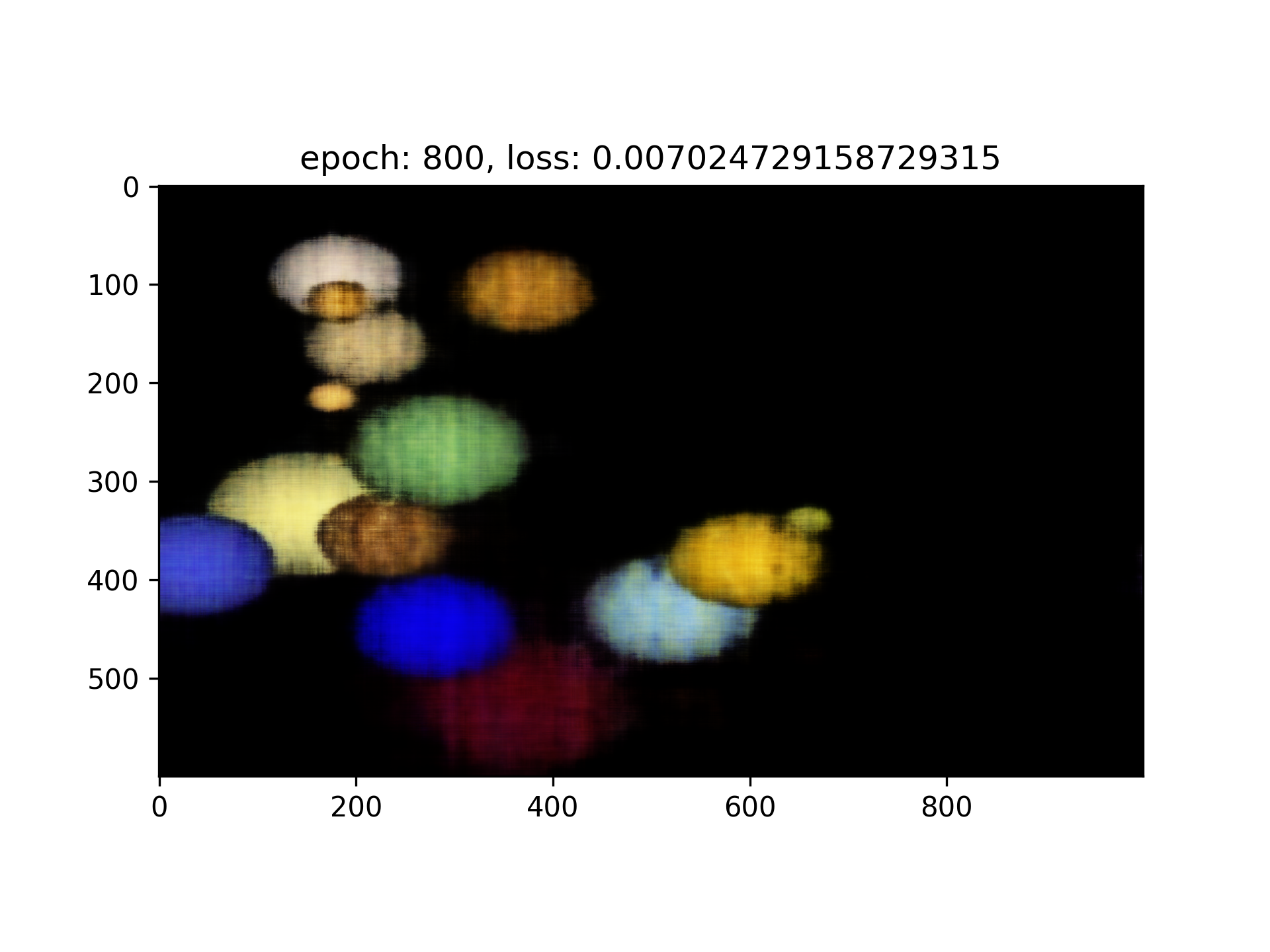
We can see that Viser shows that we are on the right track. The visualization confirms that the code is generating the desired output.

Part 2.4: Neural Radiance Field

Positional Encoding

class PosEncoding3D(nn.Module):
    def __init__(self, L):
        super(PosEncoding3D, self).__init__()
        self.L = L
        self.d_model = 6 * L + 3

    def forward(self, x):
        batch_size, num_rays_per_image, num_samples_per_rays, _ = x.shape
        result = torch.zeros(batch_size, num_rays_per_image, num_samples_per_rays, self.d_model, device=x.device)

        result[..., 0] = x[..., 0]
        result[..., 1] = x[..., 1]
        result[..., 2] = x[..., 2]

        positions = torch.arange(0, self.L, device=x.device).unsqueeze(0).float()
        
        # encoding for x, y, z
        for dim in range(3):
            result[..., 3 + dim * 2 * self.L:3 + (dim + 1) * 2 * self.L:2] = torch.sin(2 ** positions * np.pi * x[..., dim].unsqueeze(-1))
            result[..., 4 + dim * 2 * self.L:3 + (dim + 1) * 2 * self.L:2] = torch.cos(2 ** positions * np.pi * x[..., dim].unsqueeze(-1))

        return result

PE3D=\{x,y,z,\sin(2^0 \pi x), \cos(2^0 \pi x), \sin(2^0 \pi y),\cos(2^0 \pi y), \sin(2^0 \pi z), \cos(2^0 \pi z) ... \sin(2^{L-1} \pi x), \cos(2^{L-1} \pi x), \sin(2^{L-1} \pi y) , \cos(2^{L-1} \pi y), \sin(2^{L-1} \pi z) , \cos(2^{L-1} \pi z)\}

During the forward pass of the positional encoding, the input x (which represents the sampled 3D points) is transformed from [batch_size, num_rays_per_image, num_samples_per_ray, 3] into a tensor of shape [batch_size, num_rays_per_image, num_samples_per_ray, d_model]. The d_model dimensionality is calculated as 6 * L + 3.

Network: Nerf3D

class Nerf3D(nn.Module):
    def __init__(self, L_coord = 10, L_ray = 4):
        super(Nerf3D, self).__init__()
        self.L_coord = L_coord
        self.L_ray = L_ray
        self.pos_encoding_coord = PosEncoding3D(L_coord)
        self.pos_encoding_ray = PosEncoding3D(L_ray)
        self.d_model_coord = self.pos_encoding_coord.d_model
        self.d_model_ray = self.pos_encoding_ray.d_model
        self.coord_part_1 = nn.Sequential(
            nn.Linear(self.d_model_coord, 256),
            nn.ReLU(),
            nn.Linear(256, 256),
            nn.ReLU(),
            nn.Linear(256, 256),
            nn.ReLU(),
            nn.Linear(256, 256),
            nn.ReLU(),
        )
        self.coord_part_2 = nn.Sequential(
            nn.Linear(256 + self.d_model_coord, 256),
            nn.ReLU(),
            nn.Linear(256, 256),
            nn.ReLU(),
            nn.Linear(256, 256),
            nn.ReLU(),
            nn.Linear(256, 256),
        )
        self.density = nn.Sequential(
            nn.Linear(256, 1),
            nn.ReLU(),
        )  # --> density [batch_size, 1]
        self.rgb_part1 = nn.Linear(256, 256)
        self.rgb_part2 = nn.Sequential(
            nn.Linear(256 + self.d_model_ray, 128),
            nn.ReLU(),
            nn.Linear(128, 3),
            nn.Sigmoid(),
        )  # --> rgb [batch_size, 3]
        
    def forward(self, x, ray_o, ray_d):
        """
        Args:
            x: 3D coordinates. Shape: [batch_size, num_rays_per_image, num_samples_per_ray, 3]
            ray_o: Ray origin(camera location) in world coordinate system. Shape: [batch_size, num_rays_per_image, 3]
            ray_d: Ray direction in world coordinate system. Shape: [batch_size, num_rays_per_image, 3]
        Returns:
            sigmas: Density values. Shape: [batch_size, num_rays_per_image, num_samples_per_ray, 1]
            rgbs: RGB values. Shape: [batch_size, num_rays_per_image, num_samples_per_ray, 3]
        """
        # print(ray_d.shape)
        batch_size, num_rays_per_image, num_samples_per_ray, _ = x.shape
        x_pe = self.pos_encoding_coord(x)
        x = self.coord_part_1(x_pe)
        x = torch.cat((x, x_pe), dim=-1)
        x_part2 = self.coord_part_2(x)
        sigmas = self.density(x_part2)  # [batch_size, num_samples, 1]
        
        repeat_times = num_samples_per_ray
        # repeat ray_d to [batch_size, num_rays_per_image, num_samples_per_ray, 3]
        ray_d = ray_d[:, :, None, :].expand(-1, -1, repeat_times, -1)
        ray_d_pe = self.pos_encoding_ray(ray_d)
        rgb_part1 = self.rgb_part1(x_part2)
        # print(rgb_part1.shape, ray_d_pe.shape)   # --> torch.Size([1, 2500, 16, 256]) torch.Size([1, 2500, 2500, 27])
        rgb = torch.cat((rgb_part1, ray_d_pe), dim=-1)
        rgb = self.rgb_part2(rgb)  # [batch_size, num_samples, 3]
        
        return sigmas, rgb

The Nerf3D class is a neural network model used for performing 3D scene reconstruction from input images and corresponding camera parameters.

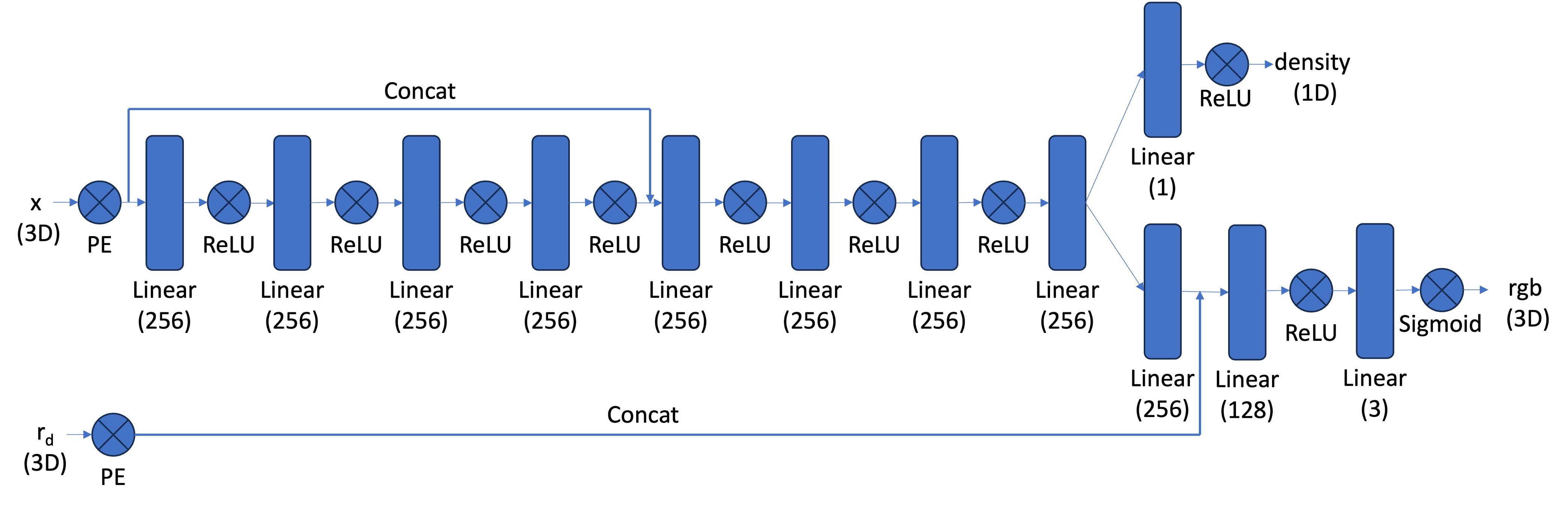
forward: Takes in the 3D coordinates (x), ray origins (ray_o), and ray directions (ray_d) as inputs. The x coordinates are passed through the positional encoding module for coordinates, and the resulting tensor is processed through the first part of the coordinate layers (coord_part_1). The encoded coordinates and the output of coord_part_1 are concatenated and passed through the second part of the coordinate layers (coord_part_2), which produces density values (sigmas).

forward (continued): The ray directions (ray_d) are expanded to match the shape of the sampled 3D points, and then passed through the positional encoding module for ray directions. The output of coord_part_2 is concatenated with the positional encoding for ray directions, and then processed through the first part of the RGB layers (rgb_part1). The resulting tensor is concatenated with the positional encoding for ray directions, and then processed through the second part of the RGB layers (rgb_part2), which produces RGB values (rgbs).

The Nerf3D model integrates density estimation and RGB prediction, allowing it to generate a complete representation of the scene from the input images and camera parameters.

Part 2.5: Volume Rendering

def volrend(sigmas, rgbs, step_size):
    """
    Volumetric rendering.
    Args:
        sigmas: Density values. Shape: [batch_size, num_rays_per_image, num_samples_per_ray, 1]
        rgbs: RGB values. Shape: [batch_size, num_rays_per_image, num_samples_per_ray, 3]
        step_size: Step size for integration. float
    Returns:
        rgb_map: Rendered RGB image. Shape: [batch_size, num_rays_per_image, 3]
    """
    alphas = 1 - torch.exp(-sigmas * step_size)
    ones_shape = list(sigmas.shape)
    ones_shape[2] = 1  # num_samples_per_ray is replaced by 1
    T_i = torch.cumprod(torch.cat([torch.ones(ones_shape, device=sigmas.device), 1 - alphas], dim=2), dim=2)[:, :, :-1, :]
    weights = T_i * alphas
    rgb_map = torch.sum(weights * rgbs, dim=2)
    
    return rgb_map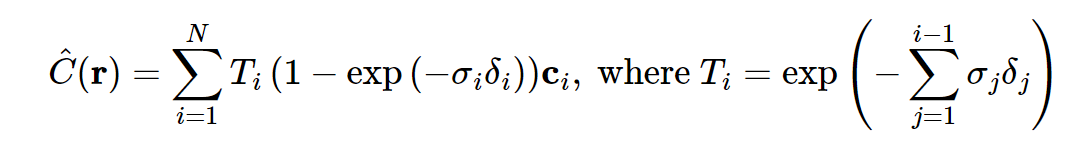

The volrend function performs volumetric rendering, which combines the density values (sigmas) and RGB values (rgbs) to generate a rendered RGB image. It calculates the alpha values (alphas) based on the density values and step size. It then computes the weights of each RGB value based on the cumulative product of the alpha values and the remaining part of the alpha values. Finally, it multiplies the weights with the RGB values and sums them up to obtain the rendered RGB image.

Train!

dataset = RaysData(images_train, K, c2ws_train)
model = Nerf3D(L_coord, L_ray).to(device)
optimizer = Adam(model.parameters(), lr=learning_rate)
loss_fn = MSELoss()
for epoch in range(num_epochs):
    optimizer.zero_grad()
    rays_o, rays_d, rays_rgb = dataset.sample_rays(max_idx = 100, ray_per_image=num_rays_per_image)
    # points: [batch_size, num_rays_per_image, num_samples_per_ray, 3]
    points = sample_points_from_rays(rays_o, rays_d, near=2.0, far=6.0, num_samples_per_ray=num_samples_per_ray, train=True)
    # no need to reshape points, because nerf3d will do this
    pred_sigmas, pred_rgbs = model(points, rays_o, rays_d)
    rend_img = volrend(pred_sigmas, pred_rgbs, step_size)
    # rend_img: [batch_size, num_rays_per_image, 3]
    # rays_rgb: [batch_size, num_rays_per_image, 3]
    loss = loss_fn(rend_img, rays_rgb)
    loss.backward()
    optimizer.step()
    print(f"Epoch {epoch + 1} Loss: {loss.item():.4f}")
    # for every 50 epochs, save the model
    if (epoch + 1) % 50 == 0:
        torch.save(model.state_dict(), f"./model/nerf3d-epoch_{epoch + 1}.pth")

Result(Novel view)

Curve

Bells and Whistles

Change background color

Function: `volrend(sigmas, rgbs, step_size, background_color)`

def volrend(sigmas, rgbs, step_size, background_color=None):
    """
    Volumetric rendering.
    Args:
        sigmas: Density values. Shape: [batch_size, num_rays_per_image, num_samples_per_ray, 1]
        rgbs: RGB values. Shape: [batch_size, num_rays_per_image, num_samples_per_ray, 3]
        step_size: Step size for integration. float
				background_color: R, G and B, Shape: [3]
    Returns:
        rgb_map: Rendered RGB image. Shape: [batch_size, num_rays_per_image, 3]
    """
    alphas = 1 - torch.exp(-sigmas * step_size)
    ones_shape = list(sigmas.shape)
    ones_shape[2] = 1  # num_samples_per_ray is replaced by 1
    T_i = torch.cumprod(torch.cat([torch.ones(ones_shape, device=sigmas.device), 1 - alphas], dim=2), dim=2)[:, :, :-1, :]
    weights = T_i * alphas
    rgb_map = torch.sum(weights * rgbs, dim=2)
    if background_color is not None:
        rgb_map = rgb_map + (1 - torch.sum(weights, dim=2)) * background_color
    
    return rgb_map

Now if the background_color parameter is passed in, we will fill in the background with color.

Part 1: Fit a Neural Field to a 2D Image

[Implement: Network]

Positional Encoding

Nerf2D network

[Implement: Dataloader]

[Implement: Loss Function, Optimizer, and Metric]

Training Result(lr=1e-2, L=10, layers = 4(default))

Metrics

Curve

[Implement: Hyperparameter Tuning]

Tuning Learning rate

Tuning Positional Encoding L & Number of layers

Training on my own image

Ground Truth

Result

PSNR Curve

Part 2: Fit a Neural Radiance Field from Multi-view Images

Part 2.1: Create Rays from Cameras

Function: transform(c2w, x_c)

Function: pixel_to_camera(K, uv, s)

Function: pixel_to_ray(K, c2w, uv)

Part 2.2: Sampling

Function: sample_rays(c2w, K, img, num_rays_per_image=10, hardcode_uv=None)

Function: sample_points_from_rays(rays_o, rays_d, near, far, num_samples_per_ray=64, train=True)

Part 2.3: Putting the Dataloading All Together

Viser Output

Part 2.4: Neural Radiance Field

Positional Encoding

Network: Nerf3D

Part 2.5: Volume Rendering

Train!

Result(Novel view)

Curve

Bells and Whistles

Change background color

Function: volrend(sigmas, rgbs, step_size, background_color)

Function: `transform(c2w, x_c)`

Function: `pixel_to_camera(K, uv, s)`

Function: `pixel_to_ray(K, c2w, uv)`

Function: `sample_rays(c2w, K, img, num_rays_per_image=10, hardcode_uv=None)`

Function: `sample_points_from_rays(rays_o, rays_d, near, far, num_samples_per_ray=64, train=True)`

Function: `volrend(sigmas, rgbs, step_size, background_color)`